arima модель – одна из популярных экстраполяционных моделей. В названии модели AR отвечает за авторегрессионную составляющую, I – за интегрированную составляющую, MA — за скользящее среднее. Каждой составляющей модели соответствует свой параметр: p, d, q. Данная модель применятся для построения прогнозов, если можно опираться только на имеющиеся фактические данные.
Задача с тремя переменными
Для начала давайте рассмотрим три составляющие модели более подробно. Авторегрессия – модель временных рядов, в которой значение временного ряда в данный момент времени может быть выражено в виде линейной комбинации предыдущих значений этого же ряда и случайной ошибки, обладающей свойством «белого шума».
Процесс скользящего среднего – текущее значение случайного процесса представляется в виде линейной комбинации текущего и прошлых значений ошибки, по своим свойствам соответствующей «белому шуму».
Интегрированная составляющая отвечает за порядок дифференциации ряда при необходимости привести ряд к стационарному. Обычно рассчитывают разницу до 2-го порядка.
Главной задачей аналитика является определение значений данных параметров. Предлагаем рассмотреть на примере определение значений параметров p, d, q. Для применения модели ARIMA необходимо иметь данные в разрезе времени любого уровня динамики (годы, месяцы, дни и т.д.). Это могут быть продажи какого-либо товара, количество заказов, клиентов и т.д.
После построения модели получится прогноз по выбранному показателю. Построенный прогноз в дальнейшем может быть использован для принятия каких-либо управленческих решений или может стать входной информацией для формирования автоматического заказа на закупку товара.
Строим прогноз с помощью Prognoz Platform
Рассмотрим данные по показателю «Индекс потребительских цен, к соответствующему периоду 2017 года по Российской Федерации». Данный показатель обычно называют инфляцией. Динамика исследуемого ряда приведена на рисунке ниже.
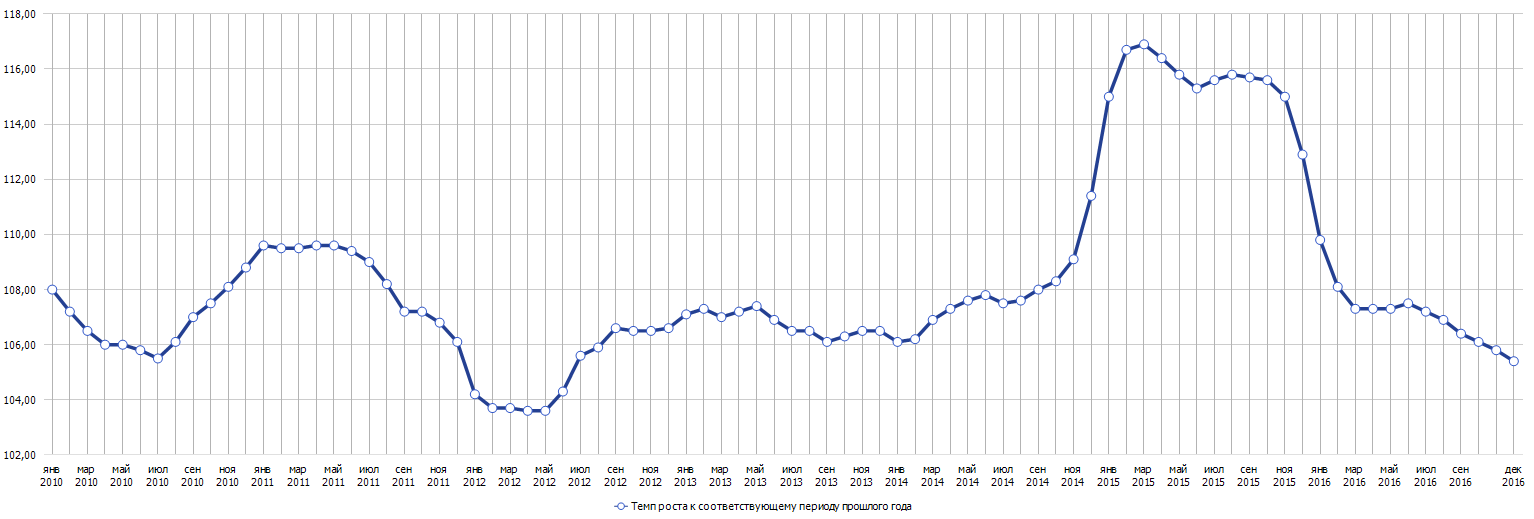
Для анализа ряда и построения ARIMA модели воспользуемся инструментом моделирования Prognoz Platform, который называется «Контейнер моделирования». Данный инструмент удобен тем, что одновременно позволяет увидеть все необходимые характеристики для построения ARIMA модели в одном окне, автоматически перестраивает модель при изменении её параметров и строит прогноз.
Также стоит отметить возможность применять преобразования к исследуемому ряду. Контейнер моделирования имеет интуитивно понятный интерфейс и позволяет строить модели без написания какого-либо кода.
Первым параметром для оценки является параметр d. Для того чтобы определить, какое значение должен принимать этот параметр, необходимо провести для ряда тест Дики-Фулера. Данный тест можно найти в меню «Анализ» Prognoz Platform, пункт «Описательные статистики».
У данного теста есть два параметра:
— Тип модели
— Дифференцирование ряда
Тип модели необходимо установить тот, который будет строиться для ряда. Мы будем строить модели с константой, поэтому выбираем пункт «С константой».
Результаты теста смотрите ниже.

Так как в столбце «Стационарность» стоит индикатор «Нет», мы можем ослабить параметр «Тип модели», выбирав «С константой и трендом», но данную модель мы рассматривать не будем, поэтому сразу установим параметр «Дифференцирование ряда» — «Дифференцированный ряд».
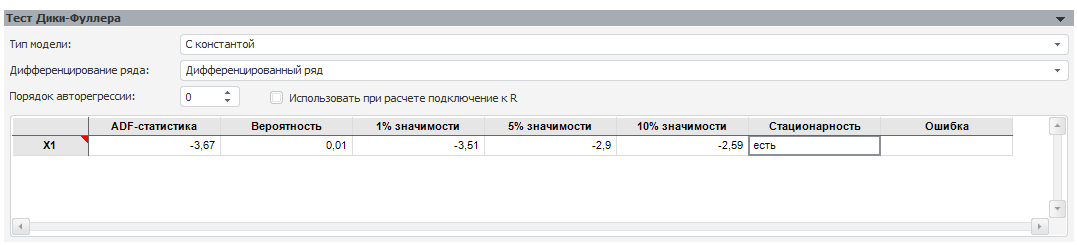
Видим, что в столбце «Стационарность» стоит индикатор «Есть», поэтому параметр d примет значение 1, так как «Дифференцированный ряд» — это разность первого порядка.
Для того чтобы выбрать параметры p, q, можно воспользоваться автокорреляционной функцией и частной автокорреляционной функцией.
Под стационарным рядом понимается временной ряд, который стабилен во времени (его среднее и прочие характеристики с течением времени не изменяются).
Таким образом, инфляция во времени оказалась нестабильна (у неё изменяются среднее и другие характеристики), а это означает, что её достаточно трудно предсказывать, и выбранный метод ARIMA может не сработать. Для этого необходимо привести ряд к стабильному состоянию, например, рассчитав разности ряда. Разность ряда рассчитывается следующим образом: из текущего года вычитаем предыдущий год.
А есть ли тренд?
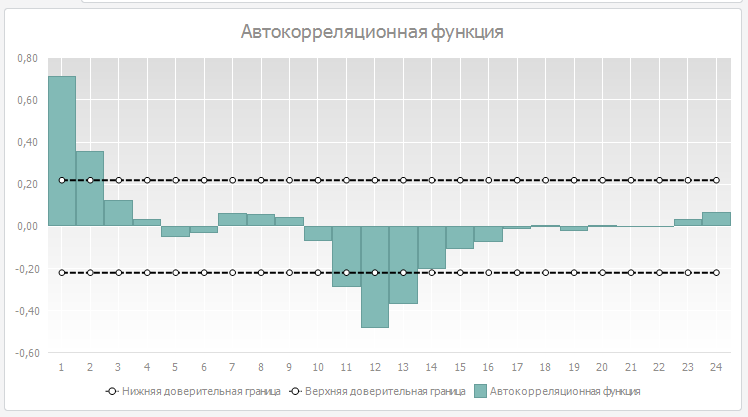
Автокорреляционная функция (АКФ) — это зависимость коэффициентов автокорреляции от лага.
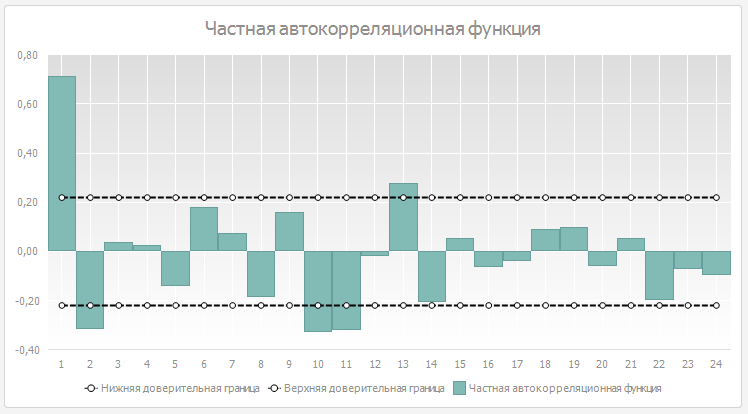
Частная автокорреляционная функция (ЧАКФ) – это зависимость частных коэффициентов автокорреляции от лага.
Рассмотрим графики АКФ и ЧАКФ для выбранного ряда. В «Контейнере моделирования» посмотреть графики данных функций можно в двух местах:
— При выборе модели ARIMA автоматически строятся данные функции.
— На вкладке «Анализ» – «Описательные статистики» – «Набор тестов». В «Наборе тестов» необходимо выбрать АКФ и ЧАКФ.
Анализируя графики функций, можно сделать вывод о наличии тренда, сезонности в ряде, а также выделить порядок авторегрессора и скользящего среднего.
Если график АКФ сходится к нулю достаточно медленно, значит, в ряду присутствует тренд. Пример расположен ниже.
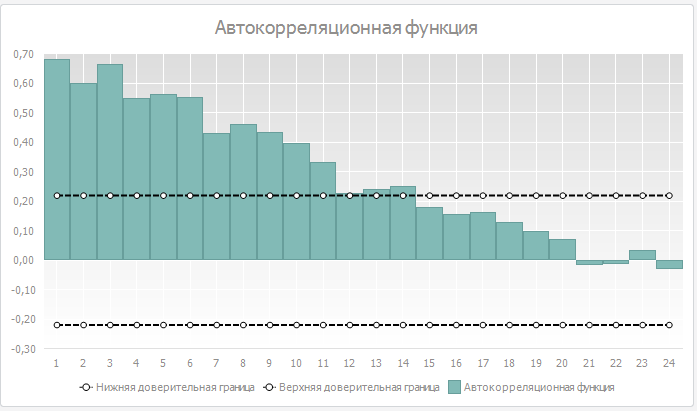
Если график сходится к нулю достаточно быстро и колеблется около него, то говорят, что присутствует процесс чистой автокорреляции.
Если на графике АКФ видны периодические всплески, значит, в ряду присутствует сезонность. Пример расположен ниже.
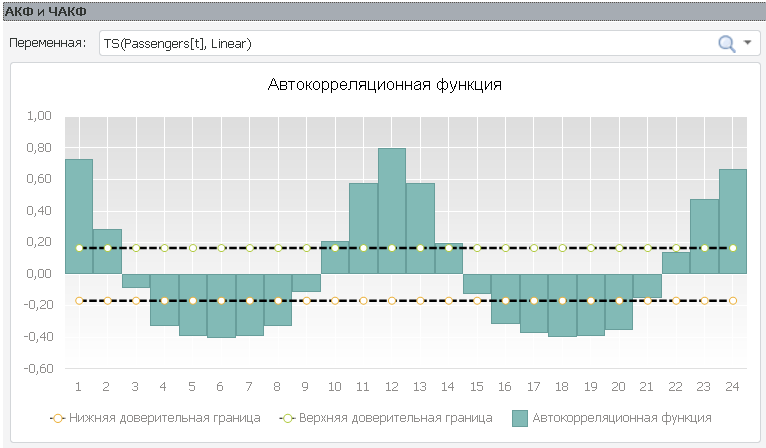
Анализируя рисунок АКФ исследуемого ряда (расположен ниже) можно сказать, что тренд в ряду отсутствует. Зато присутствует сезонность 12 порядка.
ЧАКФ отличается от АКФ тем, что не учитывает влияние промежуточных лагов при расчете частных коэффициентов корреляций. Поэтому ЧАКФ дает более «чистую картину» зависимости ряда от лага.
На лаге 1 обе функции будут иметь одинаковые значение. ЧАКФ позволяет определить порядок авторегрессора, который окажется значимым в модели.
Так, для исследуемого ряда будет значим лаг 1-го, 2-го, 10-го, 11-го, 12-го порядка.
Другими словами, можно сказать, что инфляция зависит от самой себя 1 период, 2 периода и т.д. назад.
Обе функции зависят от длины ряда. Чем больше длина ряда, тем более четко выраженными они окажутся.
Таким образом, для нашего ряда можно выделить 1, 2, 10, 11, 12 лаги. Также можно сказать, что отсутствует тренд и присутствует сезонность.
Для исследования наличия процессов скользящего среднего анализ АКФ и ЧАКФ происходит в обратном порядке. Сначала исследуется функция ЧАКФ на убывание, а затем АКФ на уровень порядка скользящего среднего.
Для нашего ряда можно будет исследовать скользящее среднее 1-го порядка.
Таким образом, для исследуемого ряда необходимо построить модели с приведенными ниже параметрами.